Leetcode Topic Digest - Linked Lists I

   leetcode 16 minutes read (About 2465 words) 0 visits

Introduction

Linked lists problems are among the most popular types of problems we often meet in all kinds of interviews. Many low-level programs, such as the dynamic memory allocator in any CPUs, use linked lists as the critical part of their implementation. You can find more details in the malloclab@CSAPP from CMU. Understanding primary problem forms and a certain degree of variant handling ability is essential. In this blog, we will be going over the most commonly asked linked problems.

Remove Linked List Elements

203. Remove Linked List Elements

Problem Description

Given the head of a linked list and an integer val, remove all the linked list nodes with Node.val == val, and return the new head.

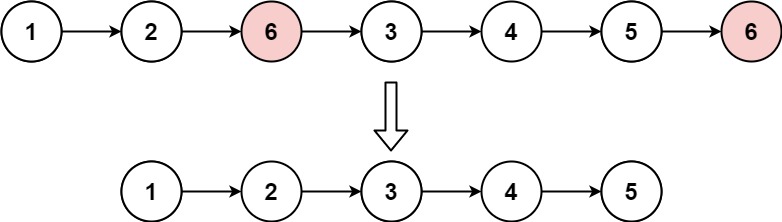
An Example of Conditional Node Removal

Pre-coding thoughts

You may want to iterate over the linked list and do something to remove the node that equals the val. So we are going to do this.

Coding Details

All the linked list-related problems assumes the following definition of ListNode

ListNode
1
2
3
4
struct ListNode {
    int val;
    struct ListNode *next;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct ListNode* removeElements(struct ListNode* head, int val) {
    typedef struct ListNode ListNode;
    ListNode *prevHead = (ListNode *) malloc(sizeof(ListNode));
    prevHead->next = head;
    ListNode *dummy = prevHead;
    while (prevHead->next) {
        if (prevHead->next->val == val) {
            prevHead->next = prevHead->next->next;
            continue;
        }
        prevHead = prevHead->next;
    }
    return dummy->next;
}

Comments

This is a fundamental linked list problem but clearly introduces the intuition behind linked list conditional removal. Also, since in C language, we don’t have OOP, thus struct is more often used. You may feel confused about the struct definition since you only see struct ListNode in the definition code; you don’t know how to call or initialize a ListNode. In fact, the struct definition has a clear rubric,

struct definition
1
2
3
4
5
6
7
struct [structure tag] {

   member definition;
   member definition;
   ...
   member definition;
} [one or more structure variables];

The ListNode above is called a structure tag. You need to define a variable before you can conveniently call a struct variable. Thus, you will find the line above

Define struct variable
1
typedef struct ListNode ListNode;

very useful. If you don’t add this line, you will need to add struct ListNode before every initialization, which requires more repetitive work. For more details on defining a struct in c, you can refer here to a well-stated tutorial.

Design Linked List

707. Design Linked List

Problem Description

This problem is more complicated in implementation than in algorithm. It asks you to design a Linked List Class using an already-defined API.

Split the API

API
1
2
3
4
5
int get(int index)
void addAtHead(int val)
void addAtTail(int val)
void addAtIndex(int index, int val)
void deleteAtIndex(int index)

Five parts are required for this design. get is pretty simple and only requires linear time complexity. All you need to do is to loop through the linked list and compare the values to each element.

myLinkedListGet
1
2
3
4
5
6
7
8
int myLinkedListGet(MyLinkedList* obj, int index) {
    MyLinkedList* currNode = obj->next;
    for (int i = 0; currNode != NULL; ++i) {
        if (i == index) return currNode->val;
        currNode = currNode->next;
    }
    return -1;
}

Since this is a singly linked list, addAtHead requires only two steps. The first is initializing the node and then attaching the node to the front of the linked list. See one possible implementation below.

myLinkedListAddAtHead
1
2
3
4
5
6
void myLinkedListAddAtHead(MyLinkedList* obj, int val) {
    MyLinkedList* dummyHead = (MyLinkedList*) malloc(sizeof(MyLinkedList));
    dummyHead->val = val;
    dummyHead->next = obj->next;
    obj->next = dummyHead;
}

addAtTail is similar. The first is initializing the new tail node, then attaching the node to the bottom of the linked list. However, there is one difference. You can not directly find the tail of a linked list. Thus you need to loop from the head node til you hit NULL.

myLinkedListAddAtTail
1
2
3
4
5
6
7
8
void myLinkedListAddAtTail(MyLinkedList* obj, int val) {
    MyLinkedList* currNode = obj;
    while (currNode->next != NULL) currNode = currNode->next;
    MyLinkedList* dummyTail = (MyLinkedList*) malloc(sizeof(MyLinkedList));
    dummyTail->val = val;
    dummyTail->next = NULL;
    currNode->next = dummyTail;
}

addAtIndex is like an insert operation in linked lists. It requires a search step and an insert step. The search step is of linear time complexity since, in the worst case, you will have to go through every node in the linked list. The insertion step requires constant time complexity. You should initialize the node with its value before insertion.

myLinkedListAddAtIndex
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void myLinkedListAddAtIndex(MyLinkedList* obj, int index, int val) {
    if (!index) {
        MyLinkedList* dummyHead = (MyLinkedList*) malloc(sizeof(MyLinkedList));
        dummyHead->val = val;
        dummyHead->next = obj->next;
        obj->next = dummyHead;
        return;
    }
    MyLinkedList* currNode = obj->next;
    MyLinkedList* dummyMid = (MyLinkedList*) malloc(sizeof(MyLinkedList));
    dummyMid->val = val;
    for (int i = 0; currNode != NULL; ++i) {
        if (i == index - 1) {
            dummyMid->next = currNode->next;
            currNode->next = dummyMid;
            return;
        }
        currNode = currNode->next;
    }
}

deleteAtIndex is the remove operation in the linked lists. It also requires a search step and a delete step. However, you should also consider the case you are asked to remove the head node of a linked list. This would mean you must remove all the nodes by free them. See implementation for details.

myLinkedListDeleteAtIndex
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void myLinkedListDeleteAtIndex(MyLinkedList* obj, int index) {
    if (!index) {
        MyLinkedList* currNode = obj->next;
        if (currNode != NULL) {
            obj->next = currNode->next;
            free(currNode);
        }
        return;
    }
    MyLinkedList* currNode = obj->next;
    for (int i = 0; currNode != NULL && currNode->next != NULL; i++) {
        if (i == index - 1) {
            // MyLinkedList* tmpNode = (MyLinkedList*) malloc(sizeof(MyLinkedList));
            MyLinkedList* tmpNode = currNode->next;
            currNode->next = tmpNode->next;
        }
        currNode = currNode->next;
    }
}

Comments

This problem helps you understand the common operations of a linked list. Its significance is more extensive for you to comprehend than to implement. However, it is a beneficial way to check your knowledge of linked lists in programming.

Reverse Linked List

206. Reverse Linked List

Problem Description

Given the head of a singly linked list, reverse the list, and return the reversed list.

An Example of Reversing Linked List

Problem Analysis

We would love it if we could reverse our linked list in one traversal. A typical method that comes to my mind when trying to manipulate the order of the linked list is Two Pointers. In this case, we start with two pointers, prev and curr. Note that prev should be initialized as NULL, because your reversed linked list will finally expect a NULL closeup.

Code Implementation

Reverse Linked List
1
2
3
4
5
6
7
8
9
10
11
12
struct ListNode* reverseList(struct ListNode* head) {
    typedef struct ListNode ListNode;
    ListNode *prev = NULL;
    ListNode *curr = head;
    while (curr) {
        ListNode *next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

Comments

It may be a little tricky for you to access the last line of code. Why are we returning prev instead of curr? Well, if you look closer at the last iteration, you will see that curr has been assigned the value of next, which in this case is NULL, while prev comes to the correct place. This is labeled as an easy problem, but you still need to watch out for the details.

Swap Nodes in Pairs

204. Swap Nodes in Pairs

Problem Description

This problem gives you a linked list, and you are asked to swap every pair nodes. See an example below.

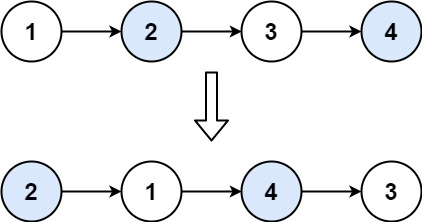
An Example of Swap Nodes in Pairs

Problem Analysis

First, we get the problem straight. It asks us to swap every neighboring pair, not every two adjacent nodes. That means you need to be aware that the step size is 2. It would be helpful to access this problem with spatial imagination. Imagine you are trying to swap two nodes in a linked list; how many steps will you take.

The answer is four steps. Assume a sample with four nodes, prev->pair_node1->pair_node2->next.

  • First, you set the prev next node to pair_node2.
  • Second, you set the pair_node1 next to next
  • Third, you set the pair_node2 next to pair_node1
  • Fourth, you update prev with the value of pair_node1 (step size is 2)

The photo below from programmerCarl demonstrates how these four steps work. Refer here for more explanation in Chinese.

ProgrammerCarl: Solution Hint

Problem Solution

Swap Nodes in Pairs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct ListNode* swapPairs(struct ListNode* head) {
    if (!head || !head->next) return head;
    typedef struct ListNode ListNode;
    ListNode* dummyHead = (ListNode *) malloc(sizeof(ListNode));
    dummyHead->next = head;
    ListNode* curr = dummyHead;
    while (curr->next && curr->next->next) {
        ListNode *node1 = curr->next;
        ListNode *node2 = curr->next->next;
        curr->next = node2;
        node1->next = node2->next;
        node2->next = node1;
        curr = node1;
    }
    return dummyHead->next;
}

Comments

This problem offers a good understanding of linked list manipulation. You will find similar problems easy to handle after you understand this problem. Next time you are asked to solve problems such as swapping nodes in threes, you will find it easy to access.

Remove Nth Node From End of List

19. Remove Nth Node From End of List

Problem Description

Given a linked list head, you are asked to remove the $N^{th}$ node from the end of the linked list.

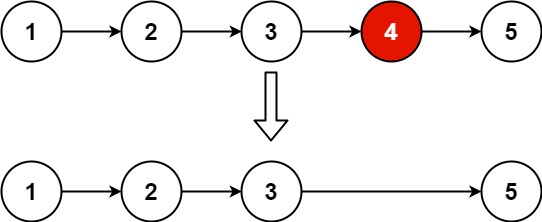
An Example of Remove Nth Node From List

Problem Analysis

This problem’s key is locating the $N^{th}$ to the last node in the linked list. There are two ways to do this. The first way is the easy-to-think-of approach. You need two loops to find the node. In the first node, you obtain the linked list’s length and calculate the node’s position to remove. The second way is a classic two pointers application.

Solution

Implementation: Two Iterations

The time complexity of removing a node from a linked list is constant. But the way to obtain the length of the linked list and search for the node in the linked list are both O(n). The total time complexity is O(n).

Two-loop Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    typedef struct ListNode ListNode;
    /* find length */
    ListNode *lengthNode = head;
    int length = 0;
    while (lengthNode) length++, lengthNode = lengthNode->next;
    /* Locate position */
    int removeIdx = length - n;
    ListNode *dummyHead = (ListNode*) malloc(sizeof(ListNode));
    dummyHead->next = head;
    ListNode *prevHead = dummyHead; // since we may change the value of `head`, we need dummyHead and prevHead to locate, replace and return
    for (int i = 0; i < removeIdx; ++i) prevHead = prevHead->next;
    /* remove Nth from the end Node */
    prevHead->next = prevHead->next->next;
    /* return curr linked list */
    return dummyHead->next;
}

Although it takes two loops, the time complexity is still bounded to O(n). In fact the submission beats 100% in time.

Implementation: Two Pointers

Two-pointers is the more natural way to solve this problem. We use a fastPointer to step one step in each iteration and a slowPointer to step ahead only when their gap satisfies n.

Two-pointer Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    typedef struct ListNode ListNode;
    ListNode* dummyHead = (ListNode*) malloc(sizeof(ListNode));
    dummyHead->next = head;
    int slowIndex = 0, fastIndex = 0;
    ListNode* slowNode = dummyHead;
    ListNode* temp = dummyHead;
    while (temp->next != NULL) {
        if ((fastIndex - slowIndex) == n) {
            slowIndex++, fastIndex++;
            slowNode = slowNode->next;
        } else fastIndex++;
        temp = temp->next;
    }
    slowNode->next = slowNode->next->next;
    return dummyHead->next;
}

Time complexity for searching the node is O(n), removing the node is constant.

Comments

If steps in problems ask you to locate an element or a node, two pointers should be your top choice.

Intersection of Two Linked Lists

02.07. Intersection of Two Linked Lists LCCI

Problem Description

Given two (singly) linked lists, determine if the two lists intersect. Return the inter­secting node. Note that the intersection is defined based on reference, not value. That is, if the kth node of the first linked list is the same (by reference) as the jth node of the second linked list, then they are intersecting.

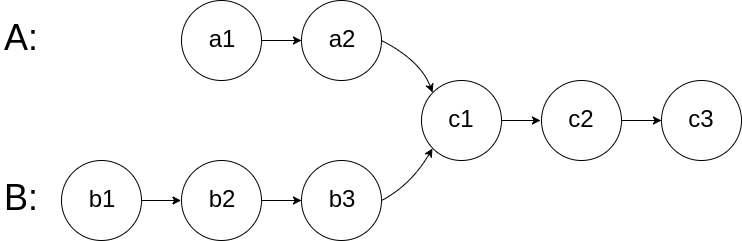
An Example of Intersecting Nodes

Problem Analysis

One thing in the description is very important. Note that the intersection is defined based on reference, not value. Which means if we look at the following example,

1
2
3
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

the intersection node is not 1, instead, it’s 8. I have read many solutions or explanations, but no one has clarified this detail. Note that there are skipA and skipB. They actually label skipA quantity of nodes to the headA as index 0. Similarly, skipB marks the skipB quantity of nodes to the headB as index 0. Thus 1 is not even in the linked lists that we are comparing.

Problem Implementation

You may find stuck in your first access. I did too. But once you get the idea, everything will be sorted out. First, you need to find the gap between the two linked lists. You can fill the gap to make them aligned with each other. After that, a linear search with a comparison will give you the answer.

Intersection of Two Linked Lists
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if (!headA || !headB) return NULL;
    typedef struct ListNode ListNode;
    ListNode* dummyHeadA = (ListNode*) malloc(sizeof(ListNode));
    ListNode* dummyHeadB = (ListNode*) malloc(sizeof(ListNode));
    dummyHeadA = headA;
    dummyHeadB = headB;
    int lenA = 0, lenB = 0;
    while (dummyHeadA) {
        lenA++;
        dummyHeadA = dummyHeadA->next;
    }
    while (dummyHeadB) {
        lenB++;
        dummyHeadB = dummyHeadB->next;
    }

    int gap = lenA >= lenB ? (lenA - lenB) : (lenB - lenA);

    dummyHeadA = headA;
    dummyHeadB = headB;

    while (gap--) {
        if (lenA >= lenB) dummyHeadA = dummyHeadA->next;
        else dummyHeadB = dummyHeadB->next;        
    }

    while (dummyHeadA) {
        if (dummyHeadA == dummyHeadB) return dummyHeadA;
        dummyHeadA = dummyHeadA->next;
        dummyHeadB = dummyHeadB->next;
    }
    return NULL;
}

Comments

This problem is about the gap-finding method and details of the implementation. It is an easy problem, but you may find it interesting and challenging to play with.

Closeup

This blog is the first edition of the Linked List Problems analysis. There will be approximately the same number of problems in the next edition. Stay tuned!

Leetcode Topic Digest - Linked Lists I

https://realzza.github.io/leetcode/Leetcode-Topic-Digest-Linked-Lists-I/

Author

Ziang Zhou

Posted on

2022-07-10

Updated on

2022-07-11

Licensed under

 

Like this article? Support the author with

Comments

Follow

follow.it

Follow my blogs for immediate feeds!

×